量子コンピュータの基本素子・量子ビットのハードウェア実装(シリコン編その4~データの書き込み・演算~)
さて、今回は量子ビットへのデータの書き込みや演算、すなわち「量子ゲート」を現実のハードウェアでいかに実現するか、という部分を解説する。これが終われば、一通り「量子ビット」の実装について説明したことになる。
もう聞き飽きたと思うが、ここでいう量子ビットの正体は、シリコンチップに閉じ込められた電子が持つ磁石(スピン)の向きだ。つまり、この記事ではスピンの向きを制御する技術について解説することになる。ポイントとなるのは、「磁気共鳴」と呼ばれる現象だ。
目次
磁気共鳴
ベクトル・モデルによる古典的説明
磁気共鳴を説明する上で、一つ注意をしたい。この説明では、今までのようにスピンを上下方向しか向けない量子力学的な磁石としてではなく、どちらを向いてもいい普通の磁石のように扱う。スピンを3次元空間の単なる矢印とみなしてしまう古典的な*1説明方法を「ベクトル・モデル」という。
以下の図のように、3次元空間にスピンが存在し、Z軸方向に静磁場がかかっているとする。実は今まで説明を避けていたが、スピンはただ単に磁場に沿って直立しているのではなく、磁場からちょっと傾いて首振り運動をしている。この運動をラーモア歳差運動という*2。
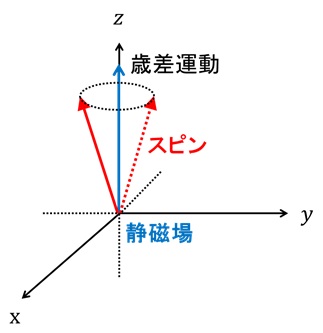
図21 ラーモア歳差運動
ラーモア歳差運動の回転周期は静磁場の強さによって変わるが、一度磁場を決めてしまえば一定である。ここで、ラーモア歳差運動の回転周期と同じ周期を持つ交流磁場を、静磁場に垂直な方向(ここではX軸方向)にかけてみよう。すると、図22のように交流磁場の軸(つまりX軸)を回転軸としてスピンが回転しだすのだ*3。このように特定の周波数を持つ交流磁場によってスピンが回転する現象を磁気共鳴と呼ぶ。そして、適当な時間だけ磁気共鳴を起こすことにより、スピンの傾きを適当に調節できる。これが、磁気共鳴によってスピンの向きを制御する、ということだ。なお、既にスピンが傾いている場合でも、交流磁場を与えれば追加でスピンを回すこともできる。
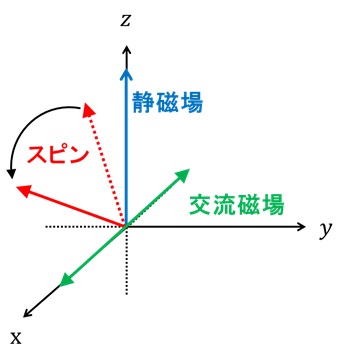
図22 磁気共鳴
エネルギー準位を用いた量子力学的説明
さて、頭を量子力学に切り替えて、同じことを説明しよう。スピンは静磁場によりゼーマン分裂を起こし、アップとダウンでエネルギーに変化がするのだった。
一方、上記で議論した交流磁場というのは、言葉を換えれば電磁波のことであり、電磁波とは量子力学的に見れば光子という粒子の集まりなのである。光子1個当たりのエネルギーは、電磁波の周波数fと、ある比例定数hの積E=hfと表される。
ここで、電子に光子を当てた時、電子スピンのアップとダウンの間のエネルギー差と、光子1個が持つエネルギーが等しいとき、電子は光子の吸収・放出現象を起こす(図23)。ダウンスピンだった場合は光子(のエネルギー)を吸収してエネルギーの高いアップスピンになり、アップスピンだった場合は光子(のエネルギー)を放出してエネルギーの低いダウンスピンに落ちる。ただし、電子と光子がうまくぶつかる確率はそれほど高くはなく、ある程度時間をかけて電磁波(光子)を与え続けることで、確率的に電子のエネルギー(スピンの向き)が変化する。つまり、電磁波を与える時間に応じて、電子のスピンがアップなのかダウンなのかという確率が変化する。このような確率の変化をラビ振動という*4。これが、磁気共鳴を量子力学的に言い直した場合の説明だ。
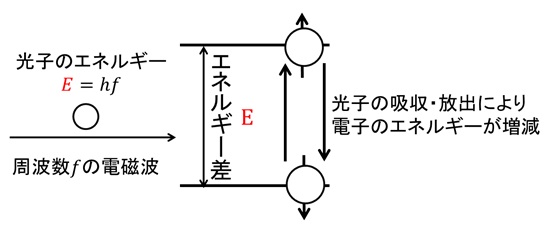
図23 量子力学的な磁気共鳴
読者の皆さんにとってどちらがわかりやすい説明だったかは分からないが、いずれにしても次の2点は押さえて欲しい
このように、ダウンスピンに初期化された電子に交流磁場(電磁場)を当て、スピンの向きをコントロールすることが、量子ビットへのデータの書き込みや演算に相当する。
スピン制御回路の実装
では、現実に実装されたチップの内部で、どうやって「磁気共鳴」とやらを起こすのだろうか。まずはチップの写真を思い出そう。
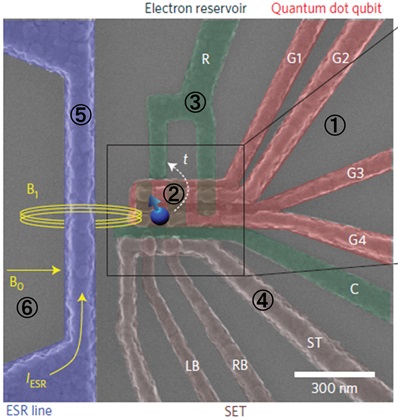
図24 SEM写真(再掲)
既に、量子ドットの中に電子が存在すること、チップ全体には横から静磁場がかかっていることは説明した。残りは、交流磁場をどのように発生させるのか、ということになる。ポイントになるのは⑤の回路だ。
簡単のため、一本の導線に直流電流を流すことを考える。この時、いわゆる「右ネジの法則」に従い、電流の周りに円形磁場が発生する(図25)。
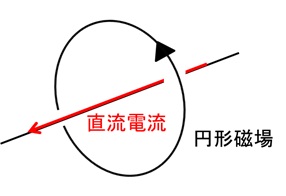
図25 円形磁場
電流の向きを反対にすると、当然この円形磁場の方向も逆転する。つまり、導線に交流電流を流すと、交流の円形磁場が発生する。
このことを頭に入れて再びチップの写真を見れば大体察しはつくかもしれない。⑤の回路に交流電流を流すと、その真横にある量子ドットには、垂直方向に交流磁場がかかるのだ(図26)。具体的な数値を出すと、ここでの交流電流の周波数はおよそ40GHzである。電磁波の言葉だとマイクロ波領域ということになる。
一方静磁場はチップに対して水平にかかっているので、磁気共鳴が起こる条件を満たしている。あとは、回路に交流電流を流す時間を調節することで、スピンの向き(重ね合わせの度合い)を適当に調節できる。
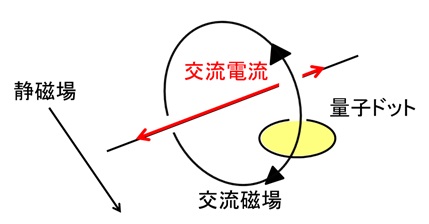
図26 交流磁場
以上の説明を読んで、スピンは具体的にどのくらいの速さで回転するのか、スピンがどのくらい回ったかを確認することは出来るのか、などといった疑問を持った人もいるかもしれないが、そのあたりの事情は次回の記事に回すことにする。
量子ゲート
ここまではスピンの制御を物理学・ハードウェアの観点から見てきたが、同じことをコンピュータ科学・ソフトウェア側の用語で表したものが「量子ゲート」だ。量子ゲートは普通のコンピュータにおける論理回路に相当し、量子コンピュータの“理論的”な基本素子である。
前述したように、スピンの方向(重ね合わせの重み)は交流電流を流す時間により自由に調節できる。このような制御を、スピンの回転角θに合わせて「θ-回転ゲート」などと呼ぶ*5。加えて、回転ゲートの中でも特徴的な性質を持つものには特殊な名前がついている。「パウリゲート」と「アダマールゲート」の2つだ*6。
パウリゲート
図27のようにΘ=π(角度の単位はラジアン)のとき、すなわち「π-回転ゲート」には、特別に「パウリゲート」という名前がついている。「ビット反転演算」とも呼ばれる。これはちょうど、アップスピンがダウンスピンに、あるいはダウンスピンがアップスピンになるので、普通のコンピュータにおけるNOTゲートに対応している。普通のNOTゲートと違うのは、入出力状態として、スピンの「重ねあわせ状態」を含むことだ(図28)。
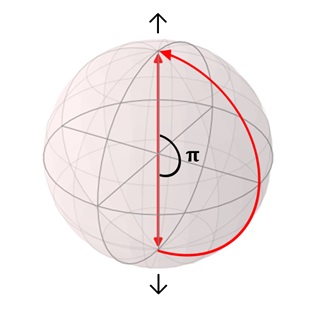
図27 ダウンスピンに対するパウリゲート

図28 重ね合わせ状態に対するパウリゲート
アダマールゲート
図29のようにΘ=π/2のとき、すなわち「π/2-回転ゲート」には、特別に「アダマールゲート」という名前がついている*7。これはダウンに初期化されたスピンを50%の重ねあわせ状態にしたり(縦に立ったスピンを横に寝かす)、逆に重ねあわせ状態のスピンをアップorダウン100%の状態に戻したりする(寝かしたスピンを起こす)効果がある。アダマールゲートには普通のコンピュータに対応する論理回路はない。重ねあわせの生成は量子並列計算の起点になり、その上いわゆる量子もつれを生成する前準備にも必要になる。アダマールゲートはまさに、量子コンピュータを象徴する演算といえる。
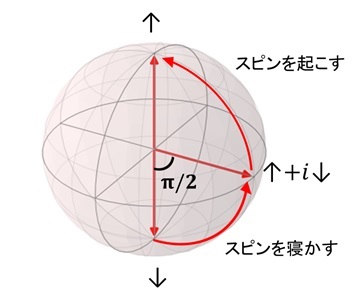
図29 アダマールゲート
量子ゲート(論理回路)はやや抽象的な概念だが、結局ハードウェアでは何が起こっているのかといえば、チップ上の回路に一定時間だけ交流電流を流しているだけなのだ。教科書には量子ゲートという抽象的な数学しか書いていないことが多く、このような現実のチップの動きについて書かれているものは少ない。
今回はここまで
量子ビットの初期化、演算、読み出しの流れは一通り説明し終わった。ここで終わりにしてもいいのだが、次回はおまけとして「量子ゲートの実装」についてもう少し深堀りしたい。
ただ、私も新生活が始まってしまい、記事を書くのに時間がかかると思う。
*1:物理学でいう「古典的」という言葉は「量子力学的でない」という意味であり、「古臭い」というニュアンスはない。
*2:これを量子力学的に説明しようとすると“位相”について詳しく説明する必要があり、話がややこしくなるので隠していた。ベクトル・モデルでは普通の3次元空間の話なので、難しく考える必要はない。
*3:本当はZ軸周りの歳差運動とX軸周りの共鳴回転が合わさり、スピンはとぐろを巻くような軌道を描くのだが、歳差運動の周期は一定なので、図ではある種の補正をかけてX軸まわりの回転だけを表示している。この補正は専門用語では回転座標系と呼ばれる。
*4:「磁気共鳴」という言葉はハードウェアとしてスピンを用いる場合に限定された用語であるのに対し、「ラビ振動」という言葉は特定のハードウェアに依存しない、より広い意味を持つ。「二準位系と場の相互作用によってラビ振動が起こる」という見方はJaynes-Cummingsモデルと呼ばれ、物理学や工学の観点から量子ビットの制御理論を語る際によく用いられる。
*5:ここでいう回転角は、厳密に言えば「量子状態ベクトルのブロッホ球上での回転角」である。スピンの場合はハードウェアの動きを表すベクトル・モデルと、量子状態の数学的な図示方法であるブロッホ球がたまたま似ているので、「回転ゲート」のイメージをハードウェアと対応させやすい。一方、例えば原子軌道を用いる量子ビットではハードウェアそのものが回転するイメージはできないが、数学的には「ブロッホ球上を量子状態ベクトルが回転する」と見なせる。
*6:制御ノットゲートやトフォリゲートといった量子ゲートもあるが、これは複数の量子ビットを組み合わせる「多入力」ゲートだ。ここで扱っている単一量子ビットで可能な量子ゲートは本質的には回転ゲートただ1種類である。
*7:理論上厳密に言えばπ/2ゲートとアダマールゲートは別物なのだが、実質的な効果が似ているので実装実験の段階ではこの2つを同一視してしまう傾向がある。専門的な話になるが、厳密な意味でのアダマールゲートを構成するにはX回転に加えてZ回転を組み合わせる必要がある。この記事ではそもそも回転ゲートにXYZの3種類があることは隠している