一見平等なトレードから必然的に不平等が生まれる(pythonシミュレーション)
池谷裕二さんの「脳はなにげに不公平」を読んでいて、初っ端から面白そうで試すのが簡単そうなお話があったので、pythonでシミュレーションしてみた。
シミュレーション内容
「100人のプレイヤー全員に1万円を渡す。100人の中からランダムに2人選び、1人目から2人目へと千円渡す。これを繰り返す」
たったこれだけだ。ただし、話を簡単にするため残金0の場合に借金はできないものとする。
全員が平等に初期資金をもらい、全員が同じようにもらう側になり、全員が同じように渡す側にもなり得る。ルールは明らかに平等だ。誰も贔屓などされていないし、誰も差別されていない。「不公平だ」なんていう文句は、この時点ではつけようがない。
シミュレーション
では実際にpythonでシミュレーションをしてみよう。プレイヤーおよびその所持金はnumpyの配列で表現する。
import numpy as np num = 100#プレイヤーの数 players = 10000*np.ones(num,np.int32)#プレイヤーを用意して10000円ずつ渡す
この時点での配列の中身を一応確認しておこう。
print("初期状態:\n",players) print("トレード前平均所持金:",np.mean(players)) print("\n") #実行結果 初期状態: [10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000] トレード前平均所持金: 10000.0
まあ当然、全員が1万円を持っている。平均が1万円なのも当たり前だろう。
次に、トレードを行う関数を作る。
#プレイやーiからプレイヤーjに1000円渡す def trade(players): i,j=np.random.randint(0,num,2)#ランダムに2人を選ぶ if (players[i] > 0):#残金があるかどうか確認 players[i]-=1000 players[j]+=1000 else: pass#プレイヤーiの残金がゼロの場合はトレード不成立
あとはトレードを繰り返せば良い。
#トレードを繰り返す times = 10000#トレードの回数 for _ in range(times): trade(players)
…わざわざ関数化する必要もなかったかも。では結果を見てみよう
print("{}回トレード後:\n".format(times),players) print("トレード後平均所持金:",np.mean(players)) print("\n") #実行結果 10000回トレード後: [ 9000 2000 19000 11000 0 7000 8000 7000 11000 5000 10000 5000 4000 20000 22000 1000 4000 3000 22000 1000 1000 19000 10000 20000 8000 3000 16000 4000 21000 1000 28000 8000 7000 0 2000 0 25000 34000 0 24000 12000 10000 34000 15000 9000 22000 19000 14000 1000 20000 2000 10000 2000 0 13000 7000 9000 22000 0 2000 24000 1000 0 2000 5000 11000 4000 0 5000 15000 3000 18000 28000 9000 21000 8000 22000 35000 11000 12000 3000 0 6000 3000 6000 8000 4000 5000 40000 1000 2000 7000 19000 0 4000 6000 7000 12000 4000 4000] トレード後平均所持金: 10000.0
数字の羅列を見てもよくわからないので、ヒストグラムにした方がよいだろう。
#ヒストグラムを表示 import matplotlib.pyplot as plt plt.hist(players)
以下のようなグラフが得られた。

なんと、たったこれだけのトレードでも「大多数の貧乏人とごく一部の大富豪」という、現実世界と同じ格差が生まれてしまったのだ!しかも恐ろしいことに、これだけの格差があったとしても「平均所持金」だけを見ると、常に10000円なのだ(当たり前だが)!平均ボーナスだとか平均貯蓄額などの数字を見るたびに現実と乖離している印象を受けるのは正規分布から大きく外れたこの格差が原因なわけだ。
まとめ
非常に平等な条件でのトレードから格差が生まれることをシミュレーションによって確認した。ちなみにこの不平等な分布はボルツマン分布と呼ばれ、数学的には自明らしい。らしいというのは、恥ずかしながら私は統計学や数理解析には詳しくなく、このような時にどう定式化すれば解析解が導けるのかという「理論屋の方法論・思考法」みたいなものがよく分からないのだ。このくらいの問題は理論計算出来る人間になりたいものだ。というわけで、この問題からボルツマン分布を解析的に導く方法をご存知の方がいたら是非教えて欲しい。
最後に、今回使用したプログラムを整理して掲載しておく。
import numpy as np import matplotlib.pyplot as plt num = 100#プレイヤーの数 times = 10000#トレードの回数 players = 10000*np.ones(num,np.int32)#プレイヤーを用意して10000円ずつ渡す print("初期状態:\n",players) print("トレード前平均所持金:",np.mean(players)) print("\n") #プレイやーiからプレイヤーjに1000円渡す def trade(players): i,j=np.random.randint(0,num,2)#ランダムに2人を選ぶ if (players[i] > 0):#残金があるかどうか確認 players[i]-=1000 players[j]+=1000 else: pass#プレイヤーiの残金がゼロの場合はトレード不成立 #トレードを繰り返す for _ in range(times): trade(players) print("{}回トレード後:\n".format(times),players) print("トレード後平均所持金:",np.mean(players)) print("\n") #ヒストグラムを表示 plt.hist(players)
量子力学によく出てくる「エルミート」って何?その物理的意味は?
はじめに
量子力学ではよく、「演算子はエルミートである」と仮定して議論を進める。そこで「エルミート演算子」あるいは「エルミート行列」について調べてみると、難解怪奇な数学理論についてはたくさん出てくるが、「ふーん。で、エルミートって、結局はどういうイミなの?」「行列がエルミートであることは、現実の物理現象とどういう関係があるの?」という部分については意外と調べても出てこない。
この記事では、私の個人的な考えではあるが、量子力学において「演算子(行列)がエルミートである」とはどういうイミを持っているのかを考察したい。
エルミート演算子の定義
まず、エルミート演算子の定義を確認しよう。
ある演算子(行列)がエルミートであるとは、自分自身と複素転置(エルミート共役)が等しいこと、すなわち
が成り立つことである。
多くの量子力学の教科書では、このエルミート演算子の数学的定義と「以下、この本に登場する演算子はエルミートである」という事実だけが告げられるのだが、せっかく物理の教科書を読んでいるのだから、どうせならその意味にまで踏み込んで説明してもらいたいものだ。
エルミート演算子の性質
これはどの教科書にも必ず書いてあるだろうが、エルミート演算子の重要な性質は「固有値が実数」であることだ。このことについての証明や解説はググればいくらでも出てくるのでここで深く説明する必要はないだろう。
「演算子がエルミートである」ことの物理的意味
以上、どこにでも書いてある事実を述べただけだが、実はこれでもうエルミート演算子の物理的意味を考察する材料は揃っている。まず、エルミート演算子の固有値は実数である。そして、演算子の固有値は測定値に対応する。なら簡単ではないか。「演算子がエルミートである」とは、要するに、「測定値は実数である」ということを言っているだけなのだ。
もう少し噛み砕いて言おう。量子力学の教科書に「演算子はエルミートである」と書いてあったら、その行間には、著者の以下のような気持ちが隠されている。
「量子力学では、波動関数が複素数だったり、演算子の係数が複素数だったり直感的には把握しにくいだろう。しかし安心してくれ。たとえ波動関数が複素数だろうがなんだろうが、君が実際に粒子の位置や運動量やスピンを測定したとき、検出器の針は必ず実数を指している。感光板の複素座標が光ることはないし、検流計に複素数の電流が流れたりすることは有り得ない。君が実際に目の当たりにする物理現象は、必ず実数の姿で現れるんだ」
実際のところ、私は学生時代に量子力学の実験を数え切れない程行ったが、実験に使っていたパルスカウンタやオシロスコープが複素数を表示したことは残念ながら(?)一度もなかった。そう考えると、「演算子がエルミートである」ことを自明の事実として受け入れるのもやぶさかではないという気持ちにならないだろうか。
「ゼロから作るDeep Learning」を読んだ(後編)
前回から引き続き、「ゼロから作るDeep Learning」の読書メモ。
4章 ニューラルネットワークの学習
損失関数
2乗差誤差はわかりやすいが、交差エントロピー誤差は直感的に意味を把握しにくい。しかしソフトマックス関数と組み合わせて使うことを考慮に入れると、幾分か理解が進んだ。
第3章で学んだ通り、ソフトマックス関数は確率を出力する。確率のlogを取るとエントロピーと呼ばれる量になるのは情報理論の基礎中の基礎だが、考えてみると誤差とエントロピーは非常に似た概念なのだ。
情報エントロピーはよく「何かデータを得た時の驚き具合」のことだと説明される。正解ラベルを提示されたとき、元々「これが答えである確率は非常に高い」と推論していたなら驚きは少ないが、「これが答えである確率は低い」と推論していたのだったら正解を知った時の驚きは大きい。この驚きを誤差と同一視しているのだろう。
さらに言えば、ここでエントロピーとしてlogを取るために、ソフトマックス関数は指数関数を使って定義されているのだろう。単純に確率に変換するだけならexpの代わりに絶対値や2乗を使っても良さそうだが、expを使えばlogとの相性がいいのは詳しく計算しなくても直感的に理解できる。
追記:
後から気づいたが、絶対値や2乗では単調増加にならないので、常に正かつ単調増加となると自然に指数関数に到達する。また、情報理論だとエントロピーの底を2にするのが自然なので、ソフトマックス関数に使う指数関数として数学的に扱いやすいexpを選び、その後それと相性がいいようにエントロピーの底をeに合わせたのかもしれない。いずれにせよ、理論がうまく設計されていることは確かだ。
20180113追記:
最近、交差エントロピーの「交差」とは何なのかを偶然知った。曰く、p×log(p)のようにlogの中身と外側に同じ変数が使われているのが普通のエントロピー。それに対して、t×log(y)のようにlogの中身と外側に異なる変数が使われているものを"交差"エントロピーと呼ぶらしい。
勾配法
ここでついに、ニューラルネットワーク(ディープラーニング)が学習を行う仕組みが明らかになった。正直に言えば、こう思った。「なんだ、ディープラーニングっつっても、結局やってることは勾配法なのか。もっと難しいものを想像していたけど、勉強してみると意外に単純なんだな」と。勾配法による評価関数の最小化(最大化)の手法自体は、全く別の分野で学んでいたのだ。それがまさか、今話題のあの「ディープラーニング」の根幹部分に使われているとは思わなかった。
そしてもう一つ私にとって重要だったのが、量子コンピュータ(特に量子アニーリング)との関連性が見えたことだ。私は量子コンピュータについては多少の知識があるのだが、人工知能についてはまったくのど素人だった。ネットで「量子コンピュータ×人工知能」といった記事を見かけても「どうせバズワード2つくっつけただけで深い意味はないだろう」と思っていた。しかし、ディープラーニングの根幹に勾配法が使われているとなると話が変わる。そのような「最適化問題」こそまさに、(アニーリング式)量子コンピュータの存在意義そのものではないか。だから「量子コンピュータ×人工知能」の組み合わせがこんなに注目されてるのか。
この点に気づいた点だけでも、本書を読んだ甲斐があった。
5章 誤差逆伝播法
誤差逆伝播のための複雑な計算が並んでいる。個人的にはもう少し厳密な証明が知りたいのだが、この本は数学の本ではないのでやむを得ないだろう。
誤差逆伝播のご利益は2つある。一つは、損失関数の微分値が(y-t)という誤差そのものに比例しているため、誤差が効率よくパラメータ更新に反映されるという点。前述したexp-logの組み合わせなどもおそらくこのためのものだろう。
そしてももう一つのご利益は、あらかじめ誤差関数の微分を(人間が)解析的に行うことによって、コンピュータの計算量が減り、計算が高速化されることだ。実際、各レイヤごとの逆伝播は「順伝搬の入力を記憶しておいて反転して出力」など、いちいち定義通りに数値微分するのに比べてはるかに簡単な処理で済んでいる。
「最初に苦労しておくと後が楽」という例は数学の他の領域でも多い。例えば対数もそうだろう。あらかじめ対数という複雑な計算を頑張っておくと、乗算が単純な加算で済んでしまう。これと同じことなのだろうと理解した。
6章 学習に関するテクニック
6章は学習に関する細かいテクニック。数学的に難解なものが多く、この本だけで理解するのは難しい。特にパラメータ更新アルゴリズムについては、いずれ原著論文などでもう少し詳しく勉強したい。
この章でもう一つ面白いと思ったのは、Dropoutとアンサンブル学習についてのコラム。異なる多数のモデルの平均値を用いるのと、一つのモデルをランダムに変化させることは同値であるというものだ。
実は、物理でも似たような概念を勉強する。統計力学や量子力学では、「たくさんの物理系を用意して一度に測定する」のと、「一つの物理系に対して時間をかけて繰り返し測定する」ことが同じ結果を与えると暗黙のうちに仮定する。いわゆるエルゴート仮説というやつだ。量子コンピュータの実験の論文では、測定がアンサンブル系で行われたのか、単一量子系で行われたのかを注意する必要がある。
7章、8章
7章は畳み込みニューラルネットワークの話。このあたりになるとさすがにゼロからの実装というのは難しいらしく、im2colなどの関数が著者によって用意されている。理論的にもやや難しく、消化不良。プーリング層によって平行移動に強くなるというのは面白いと思った。通常の意味での画像処理の勉強も合わせて、もう少しじっくり勉強したい。
8章は最新の話題や社会での応用技術についての概観。強化学習に興味があるが、文献が少ない…。
総括
後半がやや消化不良だったが、ディープラーニングとは何ぞやという概念は一通り理解できた。一冊目でここまで勉強できれば十分だろう。
「ゼロから作るDeep Learning」を読んだ(前編)
斎藤康毅著「ゼロから作るDeep Learning」を読んだので、その読書メモ。
人工知能・ディープラーニングには前々から興味を持っていてブルーバックスレベルの本を数冊読んでいたが、この分野の本格的な専門書を読むのは初めてだ。この本は有名なので、既に無数の紹介記事や書評記事が存在する。なので、この記事では書籍紹介や内容要約の体裁は取らずに、読んだときの思考をそのまま書き散らすことにする。なお、一周ざっと読んでから二週目で考えをまとめるために書いているため、思考の時系列が飛んでいるところがあるのであしからず。
1章 Python入門
私は元々物理の計算のためにPythonを使用していた経験があるので、ここは軽く読み飛ばした。Numpyで配列とスカラー値を掛け算すると配列の全要素に一気に演算が行われる仕様のことを「ブロードキャスト」と呼ぶらしい。今まで何気なく使っていたが、初めて知った。
2章 パーセプトロン
・パーセプトロンというニューロンを模したモデルにより、論理回路を構成できる。ただし、単層パーセプトロンではXORは作れない
・パーセプトロンを多層化することで、XORを構成できる。そもそも単層でNANDが構成できる時点で計算万能なのだから、適当に組み合わせればどんな回路でも作れるのは当たり前といえば当たり前だが。
20170628追記:
多層パーセプトロンの計算万能性について、自分なりにもう少し理解が深まったので追記する。
ここでは、パーセプトロンの重み(+バイアス)を適当に調節して適当に組み合わせるとNAND回路が構成できることを学んだ。NAND回路を組み合わせることにより、理論上可能な限りどんな複雑な処理でも行うことができる。
ところで、人工知能による分類問題や判断問題は、要するに膨大なif分岐だといえる。もしこういう状況ならこうしろ、もしこういう特徴ならこうだろう、といった感じだ。しかし、これを直接プログラムに書き下すのは大変だ。必要な知識をごく一部の特定の分野に絞ったものがいわゆるエキスパートシステムであったわけだが、汎用性を求めれば人間にはとても認識できないような複雑な分岐なるだろうし、そもそも明確な条件分として定義できない曖昧な判断基準もあるだろう。いかに有効な条件文を作成してそれをどう組み合わせるかが、人工知能エンジニアのノウハウだったはずだ。
しかし、どんなに複雑な処理であろうと、NAND回路を適切に組み合わせれば実現できるのだった。そして、NAND回路を組み合せるというのは、多層パーセプトロン(ニューラルネットワーク)の言葉で言えば、重みとバイアスを調節することだった(全結合だとすると、重みを0にするとノードの接続を切れるので、ノードの繋ぎ方も重みで調節できる)。どんな複雑で曖昧な判断処理の構築も、パーセプトロンの重みを調節することに帰着するのだ。
要するに、判断や分類に必要な条件文の抽出という行為が、重みパラメータという(コンピュータで扱いやすい)数値データの調節に置き換わったわけだ。
「そもそもニューラルネットワークが学習するとはどういうことなのか」「ニューラルネットワークが”何でもできる”のはなぜか」という素朴な疑問を自分の言葉で説明するとこうなる。特に、知識の獲得を数値の調整で実現する、という表現にたどり着いたのが個人的にはとても面白い。これが正解かどうかは分からないが、それなりに納得できたように思う。
3章 ニューラルネットワーク
・パーセプトロンが信号を出力(生物学用語では興奮)するかどうかを判定する関数を「活性化関数」と呼ぶ。単純パーセプトロンではステップ関数を用いるが、ニューラルネットワークでは微分ができるように滑らかな「シグモイド関数」を用いる。また、最近ではReLU(ランプ)関数なるものが多く使われるらしい。
→よく使われるということは、性能が良いのだろう。なぜReLU関数の方が性能がいいのかは、今の段階ではよくわからない。
→ReLU関数のメリットの一つは計算量が少ないこと。確かに、expを使うシグモイドに比べたら楽そうだ。だけど本当にそれだけなのだろうか?この分野では現実的な問題として計算量を減らす工夫が大事なのだから別にいいのだけど、もう少し本質的な理論上の根拠があったほうが個人的には面白い。
→いずれにしても大事なのは、活性化関数が非線形であるということ。非線形性が面白い性質を生み出すという、カオス理論や複雑系科学と同じ理屈だ。
・「行列の内積」と言われて、少し目が止まってしまった。紹介されているのは明らかに普通の「行列の積」だ。おそらく、Numpyのブロードキャストのせいで「行列の積」がdot関数に追いやられているので、勘違いしてしまったのだろう。このことはGitHub上でも訂正されている。
ちなみに、「行列の内積」というものが存在すること、それ自体は事実である。私も数学は専門ではないので墓穴を掘りたくはないが、少なくとも量子力学では以下のように習った(A、Bは複素成分で同じ大きさの行列とする)。
行列の内積の定義:
例えば
とすると、
となるので、
である。すなわち「対応する成分を掛け算して全部足す」という「ベクトルの内積」を、そっくりそのまま行列に拡張した形になる。当然、「行列の内積」でも出力は一つのスカラー値だ。
話がだいぶそれてしまった。数式を書く練習にちょうどよかった。
・重み行列と入力データを表すベクトルをかけることで、次のノードへの入力が計算できる。量子力学では普通縦ベクトルを使って行列×ベクトルと書くので、横ベクトルを使って行列が右に来る書き方はちょっと違和感がある。
・出力層では中間層とは異なる活性化関数が用いられる。回帰問題では恒等関数を、分類問題ではソフトマックス関数が用いられる。
・ソフトマックス関数の出力は「確率」と解釈できる。なぜわざわざexpを使うかだが、おそらく損失関数として使うlogと逆関数の関係になっていることが、誤差逆伝播の計算に重要だからだろう。
・ソフトマックス関数を実装する際、式変形することでオーバーフローを防ぐ。これは目からウロコだった。実装の問題は実装で逃げるしかないと思っていたが、純粋に数学的な式変形だけで根本的に解決できるのか。
・MNISTデータセットは、手書き数字の画像データの集まり。MNISTは画像認識分野のHello Worldに相当するらしい。
・数値計算のライブラリは巨大な行列の計算を効率よく行うことに最適化されているので、入力データ(ベクトル)を束ねて行列として一気に処理してしまうと、計算が大幅に速くなる。
後編に続く
量子コンピュータの基本素子・量子ビットのハードウェア実装(シリコン編おまけ~エンジニアの視点で量子ゲートを実装する~)
その1~素子構造~
その2~スピンとは何か~
その3~データの初期化と読み出し~
その4~データの書き込み・演算~
前回の記事からだいぶ時間が経ってしまった…。まあ1ヶ月は経ってないからセーフかな。
今回は量子ゲートが実際にどのように実装されているのかを現場で働くエンジニアになったつもり見てみよう。
チップの製造工場から量子ビットが実装されたチップが運ばれてきた。このチップに量子ゲートを実装したい。前回の記事で解説したように、量子ゲートとはチップに一定時間交流電流を流し、スピンを狙った角度まで回すことである。つまり、パウリゲートやアダマールゲートを実現するには実際には何秒間交流電流を流せばいいのかを知ることが、量子ゲートを実装することと同義となる。そのためには早い話、実際にチップに電流を流してみて、どのくらいの速さでスピンが回るのかを観察すれば良いのだ。その実験の様子を見ていこう。
目次
量子実験は繰り返しが基本
ひとつ注意したいことがある。このような量子力学の実験では、繰り返し測定を行う必要がある。普通に身近な物の長さや重さを測るときも、繰り返し測定することで精度を高めることはあるが、データがたった1個だとしてもそのデータには一定の意味がある。しかし量子力学の理論で扱うのは確率や期待値といった統計量であり、これはデータが1個だけではそもそも意味を持たない。「サイコロを1回振ったら3が出た」というだけで確率を語れるだろうか?今やりたいのは、「スピンがアップなのかダウンなのか」というサイコロを振ることなのだ。そのことを頭に入れておいて欲しい。
また、ここからは「初期化」や「測定」など、抽象的な言葉だけで説明してしまう部分もあるが、「実際にはチップのどの部分の回路をどのように制御しているのか」「チップの内部ではどのような物理現象が起こっているのか」という部分は、前回までの記事で解説しているので必要に応じて参照して欲しい。
実験
では、実際に実験してみよう。
今調べたいのは「交流電流をどのくらいの時間流したら、スピンがどのくらい回るのか」であったので、条件部分である「交流電流を流す時間」を変数(横軸)にして測定を行うのが自然だろう。
今までの記事で解説した通り、量子ビットの動作の流れは初期化→書き込み(スピンを回す)→読み出し(スピンの測定)の順だ。この流れを何回か繰り返し、アップスピンが観測される確率を調べる(つまり、SET回路に電流が流れ、パルスカウンタで検知される確率を調べる)*1。
さあ、まずは交流電流を0秒だけ流す(要するに流さない)。つまり、スピンをダウンに初期化したあと、間髪入れずに測定フェーズに入る。これを何回か*2繰り返し、「アップスピンが観測される確率」を計算する。すると、なんと1回もアップスピンは観測されなかった。この結果から計算される確率は、0だ*3。この結果をグラフにプロットしていこう。
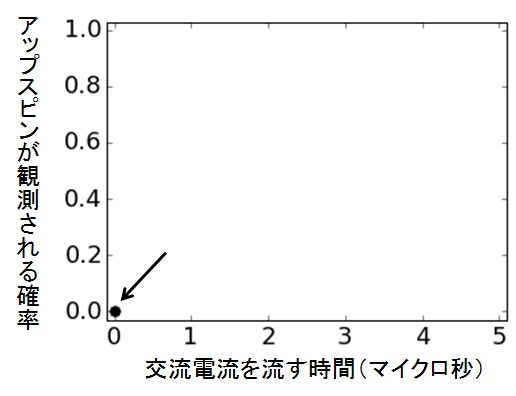
図30 実験経過1
次は0.5マイクロ秒の交流電流を流してみよう*4。今度はある程度スピンが回り、アップが観測される確率が多少は上がるはずだ。実際に何回か測定してみると、今度はおよそ15%の確率でアップが観測された。
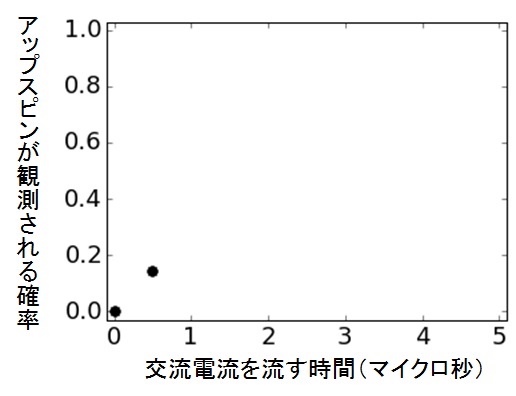
図31 実験経過2
同じことを、0.5マイクロ秒刻みで交流電流の時間を増やしながら続けていく。1マイクロ秒、1.5マイクロ秒…どんどんアップスピンが観測される回数(確率)が増えていく。
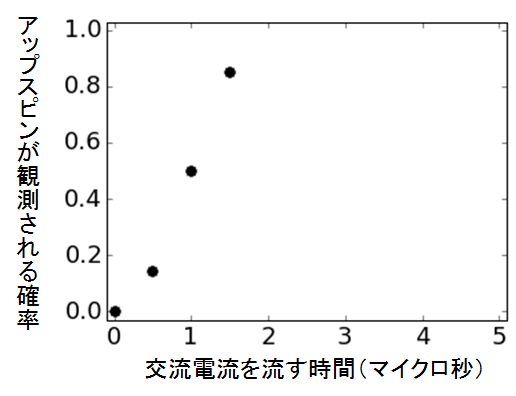
図32 実験経過3
そして、交流電流の時間が2マイクロ秒になったところで、ついにアップスピンしか観測されなくなった。アップ100%だ。さらに交流電流を長くしていくと、今度はアップスピンが観測される確率がどんどん減っていった。
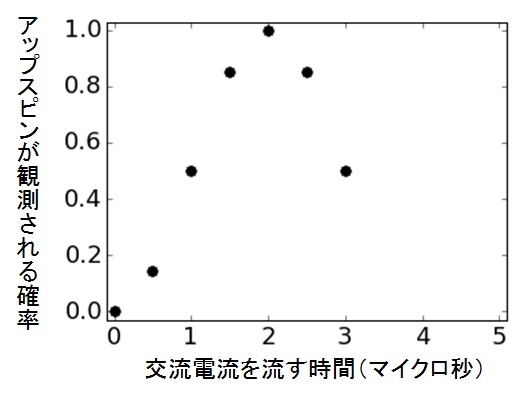
図33 実験経過4
最終的に、5マイクロ秒まで交流電流を流したときのグラフは次のようになった。
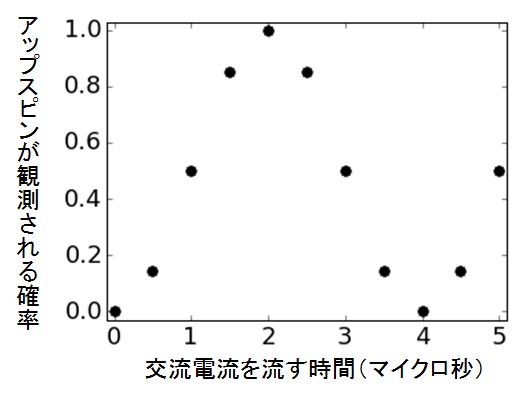
図34 実験経過5
分かりやすいように、線を引いてみよう。
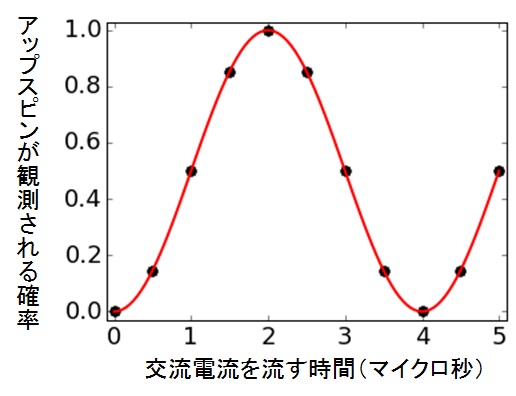
図35 フィッティング
そう、(反転)コサインカーブだ。スピンの重ね合わせの確率は、このように時間に対してコサインカーブ(別に位相のずれたサインカーブとみなしてもいいが)を描いて増減する。これがラビ振動だ*5。
実験結果を見る
この実験結果から、色々なことが分かる。まず、振動の時間周期は4マイクロ秒なので、周波数に直すと1/4=0.25MHz=250kHzだ*6。ラビ振動の周波数のことをラビ周波数という(そのまんまだ)。ラビ周波数はスピンがどれだけ速く回るか、言い換えれば量子ビットがどれくらい速く演算できるかを表す指標だ。つまり、量子コンピュータのクロック周波数だと思ってもらっていいだろう。250kHzという数字を見て今のコンピュータより遅いと感じる人もいるだろう*7。しかし量子コンピュータの計算の速さの本質はアルゴリズムにありクロックにあるわけではない。まあ速いに越したことはない、という程度だ*8。
再びグラフに戻ろう。1マイクロ秒あたりでアップとダウンが50%の重ね合わせになり、2マイクロ秒でダウンからアップに完全に反転している。つまり、アダマールゲートを行うためには、1マイクロ秒、パウリゲートを行うためには2マイクロ秒の間、交流電流を流す必要があることが分かる。このように、量子ゲートを実装するためには、一度ラビ振動実験を行い、スピンの回転速度を確認する必要があるのだ。いかにスマートなIBMであろうと、ハードウェア開発の現場ではこのような泥臭い調整作業が行われているはずだ。
量子プログラミング
ずっと交流電流を流すと言っているが、具体的には市販の実験装置使って交流信号を発生させる。例えば、こういう装置だ。
このような装置に「このくらいの周波数で、このくらいの時間だけ交流電流を流せ」と命令することで、量子ビットを駆動するのだ。このような実験装置への命令が、ある意味では最も低級な量子コンピュータ・プログラミングと言えるだろう。ちなみに、このような装置を動かすためにはC言語やPython、あるいはLabVIEW*9など普通のプログラミング言語を使う。そういう意味では、とりあえず普通のプログラミング言語が一つ使えれば、量子コンピュータを動かせると自慢してもいいだろう(笑)。
とはいえ、実験装置に直接命令する具体的な周波数値やパルス幅はチップの個性によっても変わってくるので、あまりにもハードウェア依存性が高く、量子コンピュータ・プログラミングというには低級すぎる。小規模な実験の論文では実験装置のレベル(つまり電流を何秒間流して~という感じ)でアルゴリズムを記述する「パルスシーケンス図」が使われることもあるのだが、より複雑な量子アルゴリズムを記述するときには実験装置の存在は隠蔽して「量子回路」を使うのが一般的だ。量子回路は、図のように論理の流れ(時間経過)を表す線の上に、個別の量子ゲート(論理回路)を表す記号を配置していくことで行われる。
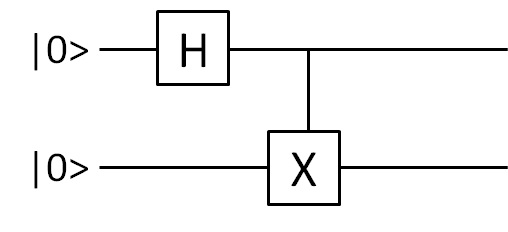
図36 量子回路の例
IBMの量子コンピュータ*10を実際に使える「Quantum Experience」でも、ユーザーは量子回路によって量子コンピュータのプログラミングを行う*11。普通のコンピュータの水準から言えば論理回路によるプログラミングも十分すぎるほど低級ではあるが、今のところこれが業界標準だ。
もちろん、高級言語の研究もされてはいるのだが、普及はしていない。最近になって「量子プログラミングの基礎」という本が出版されたらしいが、目次を見る限りではやはり数学理論の項目が並んでいる。プログラミング意味論とか、そういう分野に近い本だと思う。「苦C」や「みんPy」などと同じ感覚でこの本を開いても痛い目を見るのは確実だろう。そもそも実際のハードウェアで扱える量子ビットの数がせいぜい数ビット~数十ビット程度である現状では、C言語やPythonのような高級言語には需要がないということもあるだろう。
最後に
これで連載記事としては終わりになる。元々は学生として最後の時間に暇を持て余して書き始めたのだが、意外に時間がかかってしまった。初めてのブログ記事が連載記事というのは重すぎたかもしれない。
これからは勉強の備忘録や読書感想などが中心になると思うが、時間を見つけてこのような解説記事も書いていきたい。そのほうが自分の勉強にもなる。
*1:別に「ダウンスピンが観測される確率」を調べてもいいのだが、“信号が検出されない事象をカウントする”というのはちょっと不自然だ。どうせなら信号検出をカウントした方が気持ちいい。
*2:最低でも1万回は繰り返さないとまともに信用できるデータは取れない。
*3:実際に実験を行うと、ノイズ信号を検知してしまったり、逆に信号がロストしてしまったりするので、このような綺麗な結果になることはないのだが、さすがにそこまでリアリティを求めるつもりはない。
*4:なぜ1ナノ秒や1秒ではなく、1マイクロ秒くらいのスケールで横軸を刻んでいけばいいのだと分かったのだろう。実を言うと、スピンの回転速度はある程度理論的に予測できるし、先人の蓄積したデータも目安になる。ただ、実際のチップには個体差があるので、正確なところは手作業で確認しないと分からない。今やっているのはそういう作業という設定だ。
*5:このカーブはブロッホ球上の状態ベクトルのZ軸方向への射影成分である。そのため、ここまでで述べてきた測定のことをZ測定などと呼ぶこともある。
*6:ここでは説明しやすいように綺麗な数字になるよう調整したが、実際の論文でも大体同じくらいだ
*7:ちなみにこの記事を書くのに使っているPCのCPUは2.53GHzだ
*8:ラビ周波数はハードウェアの材料によって幅があり、速い奴だとGHzやTHz級のものもある
*9:実験や計測の分野では割とメジャーな言語
*10:IBMの量子コンピュータはハードウェアとして超伝導回路を採用しているため、ここで紹介しているシリコン量子ビットとは多少違いがある。まあやっていることは大体同じだ。
*11:その舞台裏で、ユーザーが組んだ量子回路が実験装置への命令へ翻訳され、チップに電流などが流れて演算が行われているのだ。正直アイコンを並べているだけでは量子プログラミングをしているという実感がわかないのだが、舞台裏で行われているハード側の処理を知っていると、なんとなく実感が湧かないだろうか。
量子コンピュータの基本素子・量子ビットのハードウェア実装(シリコン編その4~データの書き込み・演算~)
さて、今回は量子ビットへのデータの書き込みや演算、すなわち「量子ゲート」を現実のハードウェアでいかに実現するか、という部分を解説する。これが終われば、一通り「量子ビット」の実装について説明したことになる。
もう聞き飽きたと思うが、ここでいう量子ビットの正体は、シリコンチップに閉じ込められた電子が持つ磁石(スピン)の向きだ。つまり、この記事ではスピンの向きを制御する技術について解説することになる。ポイントとなるのは、「磁気共鳴」と呼ばれる現象だ。
目次
磁気共鳴
ベクトル・モデルによる古典的説明
磁気共鳴を説明する上で、一つ注意をしたい。この説明では、今までのようにスピンを上下方向しか向けない量子力学的な磁石としてではなく、どちらを向いてもいい普通の磁石のように扱う。スピンを3次元空間の単なる矢印とみなしてしまう古典的な*1説明方法を「ベクトル・モデル」という。
以下の図のように、3次元空間にスピンが存在し、Z軸方向に静磁場がかかっているとする。実は今まで説明を避けていたが、スピンはただ単に磁場に沿って直立しているのではなく、磁場からちょっと傾いて首振り運動をしている。この運動をラーモア歳差運動という*2。
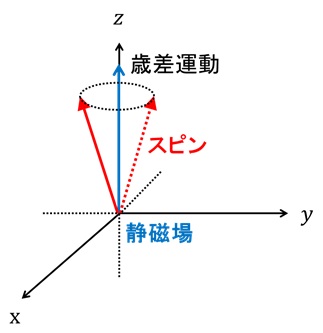
図21 ラーモア歳差運動
ラーモア歳差運動の回転周期は静磁場の強さによって変わるが、一度磁場を決めてしまえば一定である。ここで、ラーモア歳差運動の回転周期と同じ周期を持つ交流磁場を、静磁場に垂直な方向(ここではX軸方向)にかけてみよう。すると、図22のように交流磁場の軸(つまりX軸)を回転軸としてスピンが回転しだすのだ*3。このように特定の周波数を持つ交流磁場によってスピンが回転する現象を磁気共鳴と呼ぶ。そして、適当な時間だけ磁気共鳴を起こすことにより、スピンの傾きを適当に調節できる。これが、磁気共鳴によってスピンの向きを制御する、ということだ。なお、既にスピンが傾いている場合でも、交流磁場を与えれば追加でスピンを回すこともできる。
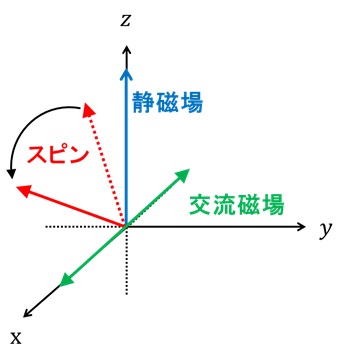
図22 磁気共鳴
エネルギー準位を用いた量子力学的説明
さて、頭を量子力学に切り替えて、同じことを説明しよう。スピンは静磁場によりゼーマン分裂を起こし、アップとダウンでエネルギーに変化がするのだった。
一方、上記で議論した交流磁場というのは、言葉を換えれば電磁波のことであり、電磁波とは量子力学的に見れば光子という粒子の集まりなのである。光子1個当たりのエネルギーは、電磁波の周波数fと、ある比例定数hの積E=hfと表される。
ここで、電子に光子を当てた時、電子スピンのアップとダウンの間のエネルギー差と、光子1個が持つエネルギーが等しいとき、電子は光子の吸収・放出現象を起こす(図23)。ダウンスピンだった場合は光子(のエネルギー)を吸収してエネルギーの高いアップスピンになり、アップスピンだった場合は光子(のエネルギー)を放出してエネルギーの低いダウンスピンに落ちる。ただし、電子と光子がうまくぶつかる確率はそれほど高くはなく、ある程度時間をかけて電磁波(光子)を与え続けることで、確率的に電子のエネルギー(スピンの向き)が変化する。つまり、電磁波を与える時間に応じて、電子のスピンがアップなのかダウンなのかという確率が変化する。このような確率の変化をラビ振動という*4。これが、磁気共鳴を量子力学的に言い直した場合の説明だ。
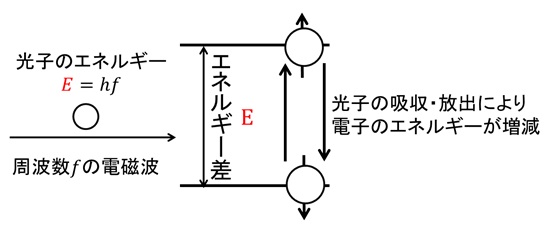
図23 量子力学的な磁気共鳴
読者の皆さんにとってどちらがわかりやすい説明だったかは分からないが、いずれにしても次の2点は押さえて欲しい
このように、ダウンスピンに初期化された電子に交流磁場(電磁場)を当て、スピンの向きをコントロールすることが、量子ビットへのデータの書き込みや演算に相当する。
スピン制御回路の実装
では、現実に実装されたチップの内部で、どうやって「磁気共鳴」とやらを起こすのだろうか。まずはチップの写真を思い出そう。
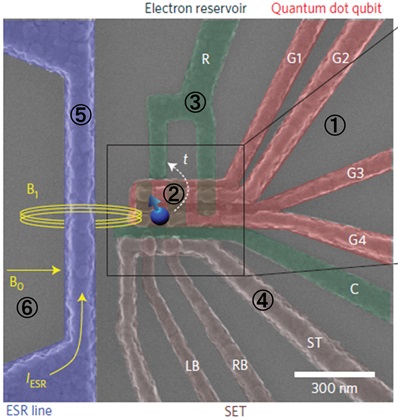
図24 SEM写真(再掲)
既に、量子ドットの中に電子が存在すること、チップ全体には横から静磁場がかかっていることは説明した。残りは、交流磁場をどのように発生させるのか、ということになる。ポイントになるのは⑤の回路だ。
簡単のため、一本の導線に直流電流を流すことを考える。この時、いわゆる「右ネジの法則」に従い、電流の周りに円形磁場が発生する(図25)。
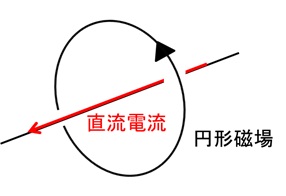
図25 円形磁場
電流の向きを反対にすると、当然この円形磁場の方向も逆転する。つまり、導線に交流電流を流すと、交流の円形磁場が発生する。
このことを頭に入れて再びチップの写真を見れば大体察しはつくかもしれない。⑤の回路に交流電流を流すと、その真横にある量子ドットには、垂直方向に交流磁場がかかるのだ(図26)。具体的な数値を出すと、ここでの交流電流の周波数はおよそ40GHzである。電磁波の言葉だとマイクロ波領域ということになる。
一方静磁場はチップに対して水平にかかっているので、磁気共鳴が起こる条件を満たしている。あとは、回路に交流電流を流す時間を調節することで、スピンの向き(重ね合わせの度合い)を適当に調節できる。
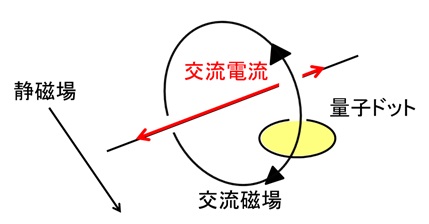
図26 交流磁場
以上の説明を読んで、スピンは具体的にどのくらいの速さで回転するのか、スピンがどのくらい回ったかを確認することは出来るのか、などといった疑問を持った人もいるかもしれないが、そのあたりの事情は次回の記事に回すことにする。
量子ゲート
ここまではスピンの制御を物理学・ハードウェアの観点から見てきたが、同じことをコンピュータ科学・ソフトウェア側の用語で表したものが「量子ゲート」だ。量子ゲートは普通のコンピュータにおける論理回路に相当し、量子コンピュータの“理論的”な基本素子である。
前述したように、スピンの方向(重ね合わせの重み)は交流電流を流す時間により自由に調節できる。このような制御を、スピンの回転角θに合わせて「θ-回転ゲート」などと呼ぶ*5。加えて、回転ゲートの中でも特徴的な性質を持つものには特殊な名前がついている。「パウリゲート」と「アダマールゲート」の2つだ*6。
パウリゲート
図27のようにΘ=π(角度の単位はラジアン)のとき、すなわち「π-回転ゲート」には、特別に「パウリゲート」という名前がついている。「ビット反転演算」とも呼ばれる。これはちょうど、アップスピンがダウンスピンに、あるいはダウンスピンがアップスピンになるので、普通のコンピュータにおけるNOTゲートに対応している。普通のNOTゲートと違うのは、入出力状態として、スピンの「重ねあわせ状態」を含むことだ(図28)。
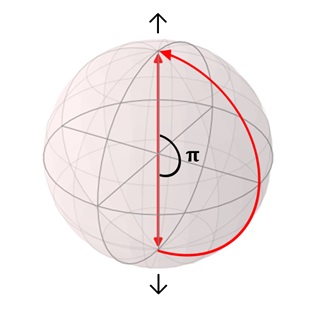
図27 ダウンスピンに対するパウリゲート

図28 重ね合わせ状態に対するパウリゲート
アダマールゲート
図29のようにΘ=π/2のとき、すなわち「π/2-回転ゲート」には、特別に「アダマールゲート」という名前がついている*7。これはダウンに初期化されたスピンを50%の重ねあわせ状態にしたり(縦に立ったスピンを横に寝かす)、逆に重ねあわせ状態のスピンをアップorダウン100%の状態に戻したりする(寝かしたスピンを起こす)効果がある。アダマールゲートには普通のコンピュータに対応する論理回路はない。重ねあわせの生成は量子並列計算の起点になり、その上いわゆる量子もつれを生成する前準備にも必要になる。アダマールゲートはまさに、量子コンピュータを象徴する演算といえる。
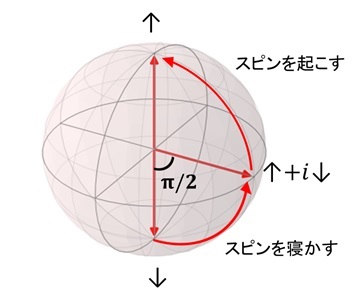
図29 アダマールゲート
量子ゲート(論理回路)はやや抽象的な概念だが、結局ハードウェアでは何が起こっているのかといえば、チップ上の回路に一定時間だけ交流電流を流しているだけなのだ。教科書には量子ゲートという抽象的な数学しか書いていないことが多く、このような現実のチップの動きについて書かれているものは少ない。
今回はここまで
量子ビットの初期化、演算、読み出しの流れは一通り説明し終わった。ここで終わりにしてもいいのだが、次回はおまけとして「量子ゲートの実装」についてもう少し深堀りしたい。
ただ、私も新生活が始まってしまい、記事を書くのに時間がかかると思う。
*1:物理学でいう「古典的」という言葉は「量子力学的でない」という意味であり、「古臭い」というニュアンスはない。
*2:これを量子力学的に説明しようとすると“位相”について詳しく説明する必要があり、話がややこしくなるので隠していた。ベクトル・モデルでは普通の3次元空間の話なので、難しく考える必要はない。
*3:本当はZ軸周りの歳差運動とX軸周りの共鳴回転が合わさり、スピンはとぐろを巻くような軌道を描くのだが、歳差運動の周期は一定なので、図ではある種の補正をかけてX軸まわりの回転だけを表示している。この補正は専門用語では回転座標系と呼ばれる。
*4:「磁気共鳴」という言葉はハードウェアとしてスピンを用いる場合に限定された用語であるのに対し、「ラビ振動」という言葉は特定のハードウェアに依存しない、より広い意味を持つ。「二準位系と場の相互作用によってラビ振動が起こる」という見方はJaynes-Cummingsモデルと呼ばれ、物理学や工学の観点から量子ビットの制御理論を語る際によく用いられる。
*5:ここでいう回転角は、厳密に言えば「量子状態ベクトルのブロッホ球上での回転角」である。スピンの場合はハードウェアの動きを表すベクトル・モデルと、量子状態の数学的な図示方法であるブロッホ球がたまたま似ているので、「回転ゲート」のイメージをハードウェアと対応させやすい。一方、例えば原子軌道を用いる量子ビットではハードウェアそのものが回転するイメージはできないが、数学的には「ブロッホ球上を量子状態ベクトルが回転する」と見なせる。
*6:制御ノットゲートやトフォリゲートといった量子ゲートもあるが、これは複数の量子ビットを組み合わせる「多入力」ゲートだ。ここで扱っている単一量子ビットで可能な量子ゲートは本質的には回転ゲートただ1種類である。
*7:理論上厳密に言えばπ/2ゲートとアダマールゲートは別物なのだが、実質的な効果が似ているので実装実験の段階ではこの2つを同一視してしまう傾向がある。専門的な話になるが、厳密な意味でのアダマールゲートを構成するにはX回転に加えてZ回転を組み合わせる必要がある。この記事ではそもそも回転ゲートにXYZの3種類があることは隠している
量子コンピュータの基本素子・量子ビットのハードウェア実装(シリコン編その3~データの初期化と読み出し~)
今回は量子ビットの初期化と読み出しについて解説する。本当は初期化→データ書き込み(演算)→データ読み出しの順で説明したかったのだが、本デバイスは設計上初期化と読み出しを切り離すことが難しいので、書き込みは後に回すことにする。
目次
初期化の必要性
既に何回も述べたように、今紹介しているシリコン量子コンピュータでは、電子のスピンを量子ビットとして用いている。スピンの向きによってデータを表すのだ。しかしスピンにデータを書き込みましょう、といっても今現在スピンの向きが分からないと制御のしようがない。実際、チップが目の前にあってもその中の電子スピンがアップなのかダウンなのか、はたまた重ね合わせ状態なのか、最初はわからないのだ(専門用語では、これを混合状態という)。なので、量子コンピュータ使用前にスピンの向きを強制的に揃える必要がある。これが量子ビットの初期化だ。普通のコンピュータで言えば、メモリに強制的に一律のデータを上書きする、物理フォーマットに相当する。ただし、量子ビットは極めて不安定であり、せっかく初期化しても使用せずに放っておくだけですぐにまたスピンの向きがわからなくなる*1。そのため、量子ビットを使おうとする度にまずは初期化をする必要があるのだ*2。
なお、ここから先の説明はそれなりに難しくなる。理屈抜きにとにかく「何をしたらどうなるのか」が手っ取り早く知りたい方は、上記目次から最後のまとめの部分に飛んでもらいたい。
自然はエネルギーが低い方に行こうとする
具体的な話を始める前に一つだけ頭に入れておいて欲しいことがある。
それは、「自然はなるべくエネルギー(より正確にはポテンシャル・エネルギー)が低い方に行こうとする」ということだ。例えば、高いところにある物が落下するのは、位置エネルギー(ポテンシャル・エネルギーの一種)が低い方が安定するからだ。そもそも、量子ドットに電子が閉じ込められているのも、(ポテンシャル・)エネルギー箱の底にハマっているからだった。また、D-Wave量子コンピュータについて調べたことがある方は、以下のような図を見たことがあると思う。D-Waveの動作原理である量子アニーリングも、量子が自動的にエネルギーの低い方へ向かうことを利用しているのだ。
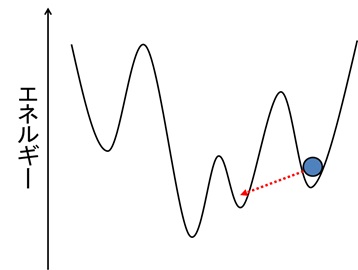
図9 エネルギーが低い方に落ちていく
スピンの初期化
やっと本題に入ることができる。まったく分からないスピンの向きを、実際にはどのように揃えるのだろうか。まずは以前にお見せしたチップ素子の写真を再掲しよう。

図10 SEM写真(再掲)
初期化の説明に必要なのは、①量子ドット構成用電極のうちG4電極と、②量子ドット、それから③貯蔵電極だ。
ここで、量子ドット(の中の電子)と貯蔵電極(の中の電子)のエネルギーを比較してみよう。
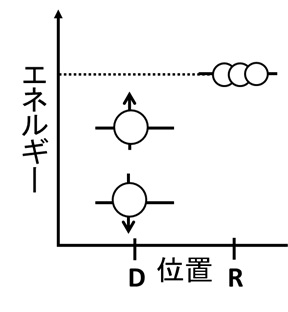
図11 エネルギーの比較
横軸のDは量子ドット、Rは貯蔵電極の位置を表している。量子ドット(D)よりも貯蔵電極(R)の方がエネルギーが高いことがわかる*3。なお、量子ドットには電子は1つだけだが、貯蔵電極には電子が大量に存在しており、「電子の池」状態になっている。
ここで、量子ドット近くにある電極G4の電圧を適当に調節して、アップスピンのエネルギー>貯蔵電極のエネルギー>ダウンスピンのエネルギーとなるように、量子ドットのエネルギーを底上げしてみよう。
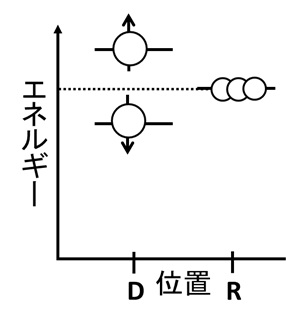
図12 量子ドットのエネルギーを上げる
今、スピンはアップなのかダウンなのかまったく分からないので、場合分けして電子の振る舞いを見ていこう。
ダウンスピンの場合
この場合、特に何も起こらない。ダウンスピンはエネルギーが低いため、電子は安定しているのだ。
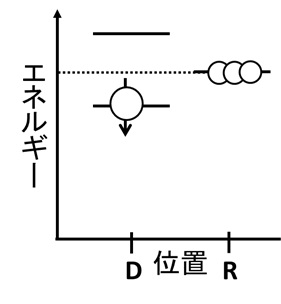
図13 ダウンスピンでは何も起こらない
アップスピンの場合
では、スピンがアップだった場合を見てみよう(図14左)。ここからが見ものだ。
前述したように、自然はエネルギーが低い方に進む。図を見て察した方もいるかもしれないが、スピンがアップの場合、エネルギーが高く居心地の悪い量子ドットから、よりエネルギーの低い貯蔵電極の方に移動するのだ。もちろん、このとき一時的に量子ドットは空になる。この現象は自然に起こるので、電極G4電圧の調節後、ただ待っているだけで良い(具体的には100マイクロ秒程度)。
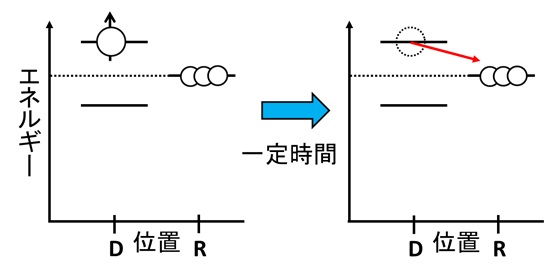
図14 アップスピンでは、貯蔵電極の方が安定
次の説明が初期化を理解する最後の山場だ。既に述べたように、貯蔵電極の中には電子がたくさんいる。量子ドットが空になってから時間が経つと、貯蔵電極の中の電子のうち、たまたまダウンスピンを持っているものが1つ、量子ドットに移動してくるのだ(図15右)*4。なぜなら、ダウンスピンの電子にとっては、貯蔵電極にいるより、量子ドットに入った方がエネルギーが低いからだ。この現象も、ただ100マイクロ秒待っているだけで自然に起こる。
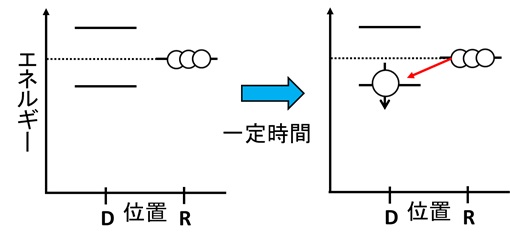
図15 時間が経つと、量子ドットに電子が戻ってくる
ぐちゃぐちゃ説明したが、結局何をしたかというと、量子ドット付近の電極の電圧を調節してから、ただ時間が経つのを待っていただけだ。電子がダウンスピンだと何も起こらず、アップスピンだった場合には電子が貯蔵電極に逃げ、空になった量子ドットにダウンスピンの電子が入ってくる。最初のスピンの向きがどちら向きであろうが、最終的にスピンはダウンになっている。つまり、スピンがダウン状態に初期化された、ということだ。もちろん、一連の処理が終わったら電極の電圧を再調整し、量子ドット内のエネルギーが貯蔵電極に比べて低い状態に戻す。このようにして、データの書き込みや演算の準備が整う。
ちなみに、チップを製造してから初めて量子ドットに電子を注入する際にも、まったく同じ仕組みが適用できる。
データの読み出し
では次に、量子ビットのデータ読み出しに移ろう。スピンは初期化されたあと、何らかの演算が行われ(演算については次回の記事で説明する)、何らかの重ねあわせ状態になっているものとする。重ねあわせ状態にあるスピンを観測すると、重ねあわせの確率に従い、アップかダウンのどちらかが観測値として得られる。これが教科書的な筋書きだ。では、現実のデバイスでは、そのような観測をどのように実現するのだろうか。ポイントになるのは、チップ素子写真の④、「単電子トランジスタ」の機能だ。その説明のため、まずは「普通のMOSトランジスタ」の動作原理から入るのが良いだろう。
MOSトランジスタ
とはいえ、MOSトランジスタの動作原理はネットで調べればいくらでも出てくるので、軽い説明で十分なはずだ。pnp型のMOSトランジスタは、図のように、正に帯電したP型半導体に、負に帯電したN型領域が埋め込まれた構造をしている。
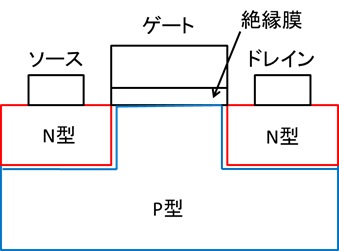
ここで、ソース電極とドレイン電極の間に電圧をかけても、N型領域とP型領域の境目には大きなエネルギーの壁があり、電子はその壁を越えられないため、電流は流れない。ここで、ゲート電極に正の電圧を加えると、ゲート電極の真下にP型領域内の電子が集まり(絶縁膜があるので外に流出することはない)、この部分が負に帯電して一時的にN型領域が形成される。そのため両端のN型領域が繋がり、電流が流れるようになる。これが、MOSトランジスタの大まかな原理だ。
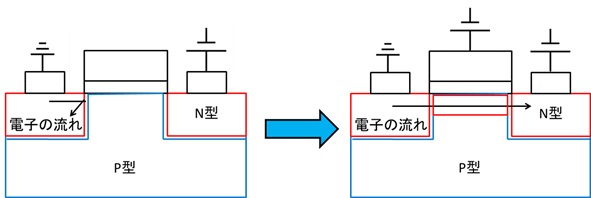
単電子トランジスタ
次に、単電子トランジスタ(以下SET)の動作原理を説明する。図はチップ写真のSET部分を拡大したものだが、これ見てもわかるように、量子ドットとSET回路はかなり近い位置にある。これがポイントだ。
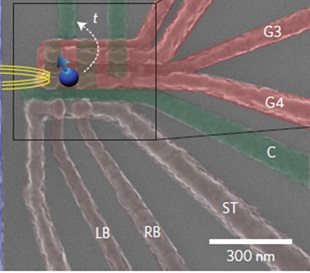
図18 SET部分拡大
図のように、SET回路の端に電圧をかける。当然、電子は左から右に流れようとする。しかし、量子ドットに電子が入っていると、ドット内の電子とSET回路に流れる電子が電気的に反発するため、SETに電流が流れないのだ。ドット内の電子による電気的バリアはクーロン障壁と呼ばれている。一方、量子ドットから電子がいなくなると、クーロン障壁がなくなるので、SETに電流が流れる。
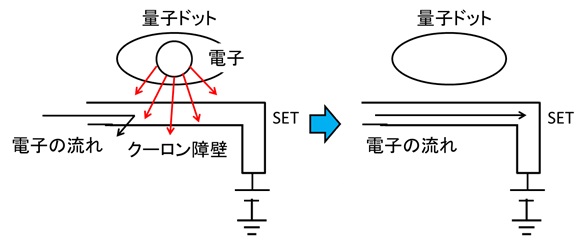
図19 単電子トランジスタの動作原理
ここで、初期化のことを思い出していただきたい。量子ドット内の電子がダウンスピンならドット内に留まり、アップスピンだったら貯蔵電極に逃げるのだった。つまり、ドット内の電子がダウンスピンのときにはSETに電流が流れないが、アップスピンの場合SETに電流が流れる。SETに電流が流れるかどうかを検知することで、ドット内の電子がアップスピンだったのかダウンスピンだったのかを判定できるのだ*5。これも前述したことだが、量子ドットが空になってから大体100マイクロ秒で電子が再びドットに入り、SETの電流は止まる。この100マイクロ秒程度のパルス電流は、I/Vコンバータで電圧パルスに変換され、パルスカウンタなどの装置でカウントされる(そのあとはコンピュータで統計処理などが行われる)。これが、「スピンを観測する」ということの正体だ。
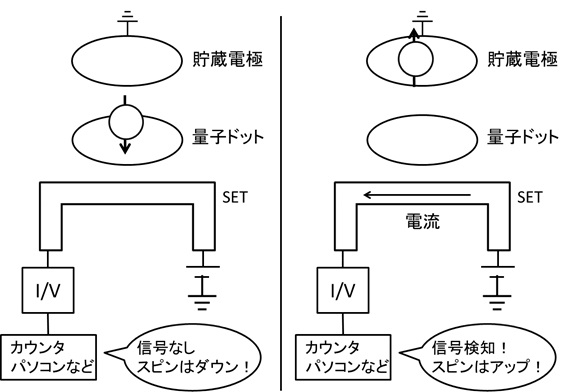
図20 スピンの観測
加えて、観測後にスピンは自動的にダウンになることにも注目したい。この記事の最初の方に、量子ビットを使う前には必ず初期化が必要であると述べた。このデバイスでは、データの読み出し時に自動的に初期化が行われるため、必要であれば測定後すぐに次の演算に移ることができるのだ。
まとめ
話が長くなってしまったので、「初期化と読み出し」には結局何をすれば良いのかをまとめておこう。
1.量子ドット付近の電極G4の電圧を調節する
2.一定時間待つ
もし電流が流れなかったら→電子はダウンスピンだったことが分かる
もし電流が流れたら→電子はアップスピンだったことが分かる
3.一定時間待つことにより、自動的にダウンスピンへの初期化が行われる
4.必要なら次の演算を行う
5.1に戻る
量子力学なんて所詮ただのテクノロジーだ
量子力学の話になると、やたらと観測という言葉が一人歩きしている感がある。場合によっては人間の主観や意識などの哲学的領域に話が及ぶこともある。量子力学を魔法のような学問だと思っている人もいるらしい。このような現実に動作するデバイスの仕組みを知ることによって、「量子力学なんて所詮ただのテクノロジーなんだ」と多少なりとも現実味を持っていただければ幸いである。
最後に
さて、次回は量子ビットへのデータの書き込みおよび演算の仕組みを解説する。もしかしたら、量子ゲートまで話に加えるかもしれない。
*1:いわゆるデコヒーレンスと呼ばれる問題。この記事では扱わないが、いずれデコヒーレンスについての解説記事も別に書きたいと思っている。
*2:初期化については量子力学や量子コンピュータの教科書には殆ど記述がなく、アルゴリズムの章などでは「N個の量子ビットが|0>状態に準備されているとする」などと、最初から量子ビットが初期化されている前提で話が進むことが多い。しかし、実際のデバイスを動作させる上で、初期化は非常に大事なプロセスだ。初期化の精度が中途半端だと、そのあとの全てのプロセスが信用できないものになってしまう。量子コンピュータのハードウェア技術者を目指す方は、このような教科書に載っていない部分についても意識しておいた方がいいだろう。
*3:正確には、貯蔵電極のエネルギーは「帯」になっているのだが、ここではフェルミ準位のみに簡略化している。
*4:エネルギーが低い方に落ちていくなら、量子ドット内でアップスピンからダウンスピンに直接落ちたりはしないのだろうか。もちろん、それも可能ではある。しかし、ここでは説明していない専門的な理由により、貯蔵電極に落ちていく確率の方がはるかに高い。
*5:電流が流れたかどうかだけ判断できれば良いので具体的な数値にあまり意味はないが、このとき流れる電流の大きさは大体500ピコアンペア程度である。
